venerdì 7 settembre 2018
giovedì 6 settembre 2018
EQUAZIONI DIOFANTEE
Sono equazioni a coefficienti intere e delle quali si cercano soluzioni intere.
Consideriamo quelle lineari in x e y del tipo ax+by=c.
Posto d=MCD(a, b) queste equazioni hanno soluzioni solo se d divide c.
Se l'equazione ha soluzioni allora ne ha necessariamente infinite e sono date dalla somma di una soluzione particolare (x', y') e di una generica dell'equazione omogenea ax+by=0.
Ad esempio 3x+4y=5 ha come soluzione particolare (3,-1). La soluzione dell'equazione dell'omogenea 3x+4y=0 è (4t,-3t). Quindi la soluzione è (4t+3,-3t-1).
Consideriamo quelle lineari in x e y del tipo ax+by=c.
Posto d=MCD(a, b) queste equazioni hanno soluzioni solo se d divide c.
Se l'equazione ha soluzioni allora ne ha necessariamente infinite e sono date dalla somma di una soluzione particolare (x', y') e di una generica dell'equazione omogenea ax+by=0.
Ad esempio 3x+4y=5 ha come soluzione particolare (3,-1). La soluzione dell'equazione dell'omogenea 3x+4y=0 è (4t,-3t). Quindi la soluzione è (4t+3,-3t-1).
Graficamente le soluzioni dell'equazione Diofantea sono i punti a coordinate intere che appartengono alla retta. Ad esempio le soluzioni dell'equazione 2x+3y=5 sono del tipo (1,1) soluzione particolare + (3t, -2t) soluzione omogenea. Quindi sono soluzioni tutte le coppie (1+3t,1-2t) al variare di t nei numeri interi. Ad esempio per t=1 ottengo C(4,-1) (vedi figura)
video lezione
martedì 4 settembre 2018
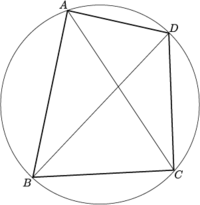
QUADRILATERI CICLICI
Un quadrilatero si dice ciclico se si può iscrivere in una circonferenza.
1)Un quadrilatero è ciclico SE E SOLO SE gli angoli opposti sono supplementari.
DIM: è conseguenza del fatto che l'angolo alla circonferenza è la metà dell'angolo al centro.
2) Un quadrilatero è ciclico SE E SOLO SE sono uguali gli angoli che "insistono sullo stesso lato"
Un quadrilatero è ciclico SE E SOLO SE vale il teorema di TOLOMEO
TEOREMA DI TOLOMEO: ABXDC+ADXBC=ACXBD
Un quadrilatero è ciclico se e solo se (vale T. corde)
AOxOC=BOxOD
Iscriviti a:
Post (Atom)